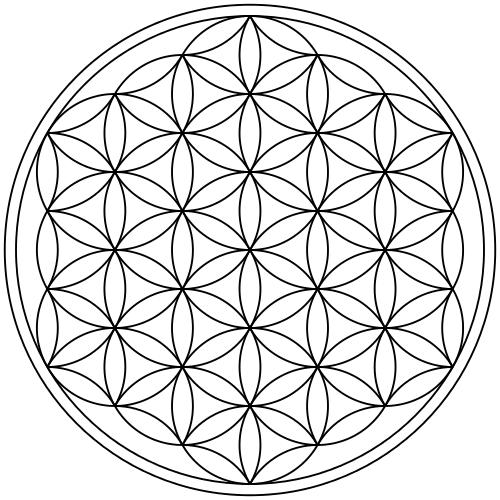
From a plane to the Flower of Life

The formation of the FOL is easy. First, we have one circle (centered at point A) on a plane. Then we interlock another circle (centered at point B) with the first one by intersecting both circles through their centers on the same plane:

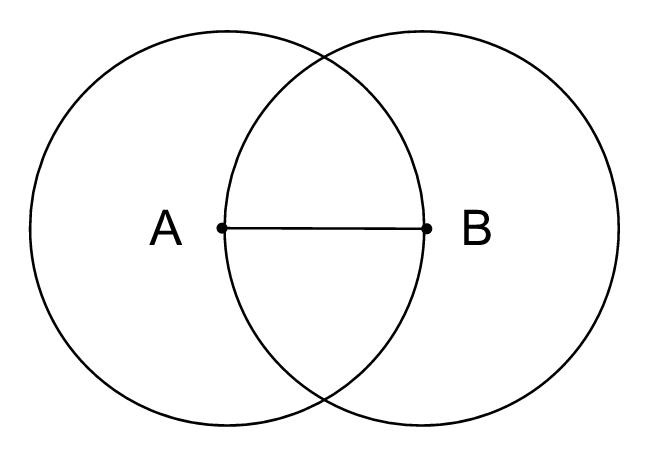
This figure is known from Old Babylonian times as an Ox-eye (igi.gu₄¹), and it can be seen as a primary generator of well-defined geometric forms. The lens-like part in the middle has various names such as Vesica Piscis (bladder of a fish), womb / female vulva, and mandorla (almond) that brings us back through a botanical connection to the symbology of the formation of the FOL. Symmetrical figures outside of the oval central shape are called lunes² in geometry and they resemble waning and waxing phases of the Moon.

Rhombus

Another geometrical figure constructed to the intersection points in the middle is a quadrilateral rhombus, which is shown below:

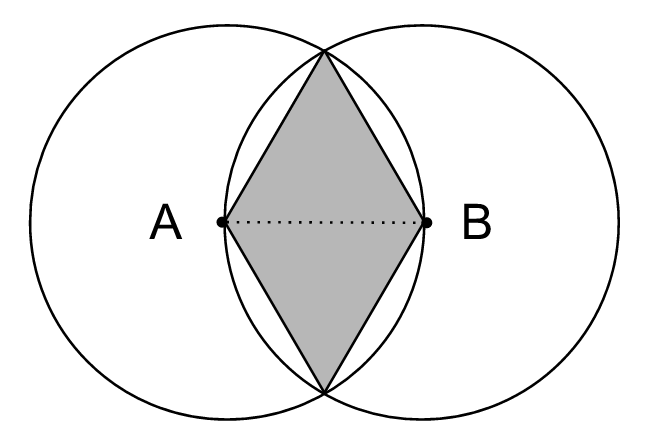
This shape (or thinner lozenge version) has been used on temple mosaics in the ancient Sumerian city of Uruk IV (3400 – 3100 BC) as already mentioned in my previous research³. Rhombus (gan illar⁴, a bow as denoted by Old Babylonians) can be seen as two equilateral triangles face to face. We often can find this symbol often on mosaics and paintings, too. Below is a part of the geometrical work on the walls of the ancient synagogue in Sardis⁵:

By adding one circle to the intersection point C, a triangular wedge shape becomes even clearer:

2300 years ago this figure was studied by Euclid in his book Elements Book 1, Proposition 1⁶. From previous etymological notes, we remember how cuneiform language is written with a reed stylus sharpened to a triangular shape in one end. This is why the whole cuneiform writing system is in the center of the early formation of the FOL. The curved triangular shape in the middle is called Reuleaux triangle⁷, which has also been studied by Leonardo da Vinci. What did he not study?!

Another shape that is continuously used in religious context in various cultures to symbolize trinity, is an interlaced triquetra⁸, or a trefoil knot which is shown above.

Square root of 3

The further procedure to create the FOL is simply repeating: 1) finding a center for a new circle from the previous circles' intersecting points and 2) adding a new circle on it. Let us add a circle (at point D) to the figure:

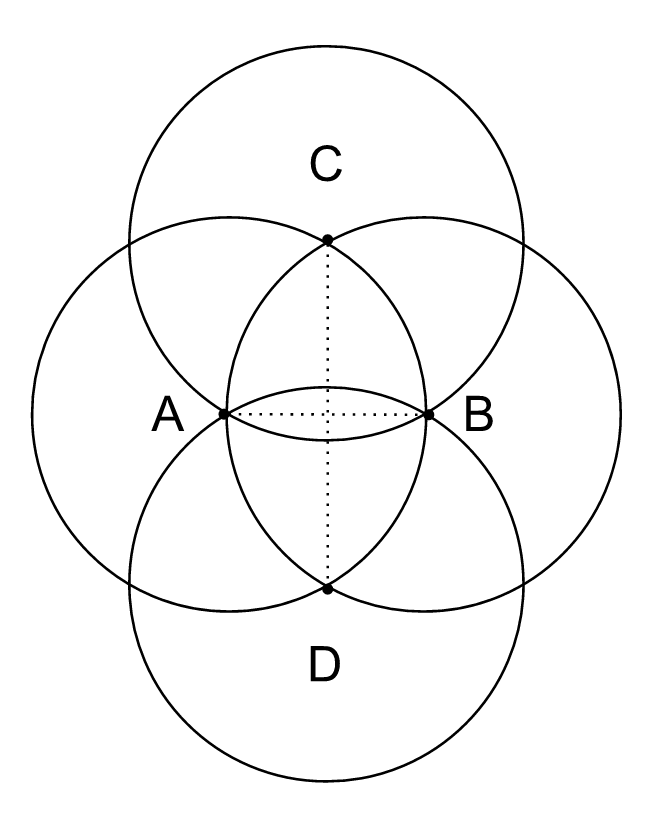
We can see two other features appearing at this point. A smaller lens or leaf is at the center of the Vesica Piscis between points A & B. When multiplied these leaves becomes six petals on the rosette. Another feature is a mathematical relationship between lines CD / AB which is known to be the square root of 3 ( ) or "a measure of a fish". Origin of the latter term or its possible relation to the allegorical story of 153 fish⁹ in the New Testament¹⁰ has faded to the history. But we know that Archimedes used the ratio as a lower limit estimation for the square root of 3. He used this ratio to further estimate the relationship between a circle's diameter and its circumference - the so famous pi () - giving it a practical value of (or ).

Already from the Old Babylonian times, it is known that people tended to give descriptive names for all possible geometrical figures. Ideas for names were derived from everyday objects. A good example is a form called Arbelos¹¹ or "Shoemaker's knife" which was studied by Archimedes in 250 BC. Ancients before Archimedes did not have mathematic symbols like we have today. Instead, they used rhetorical algebra¹² and everyday words for geometric shapes, which also often had mystical properties within their belief systems.

Thus, the name and the meaning of the square root of 3 could have been associated with the fishes. Yet, the square root of 2, or halving and doubling, could have been associated with the bread. See for example "grain-field" or "barge" that are terms used in Babylonian mathematics¹³. But more interesting is the fact that the square root of 3 is not only the ratio inside Vesica Piscis, but also the diagonal of the cube compared to the side of the cube. Unfortunately going more deep into the third dimension is not in the scope of this document. This is just another example how ideas of higher dimensions are present in lower dimensions.

Six-petal rosette

The naming of the FOL is speculated later on in the document Part 2, so let us finalize the figure by adding circles with center points E, F, and G:

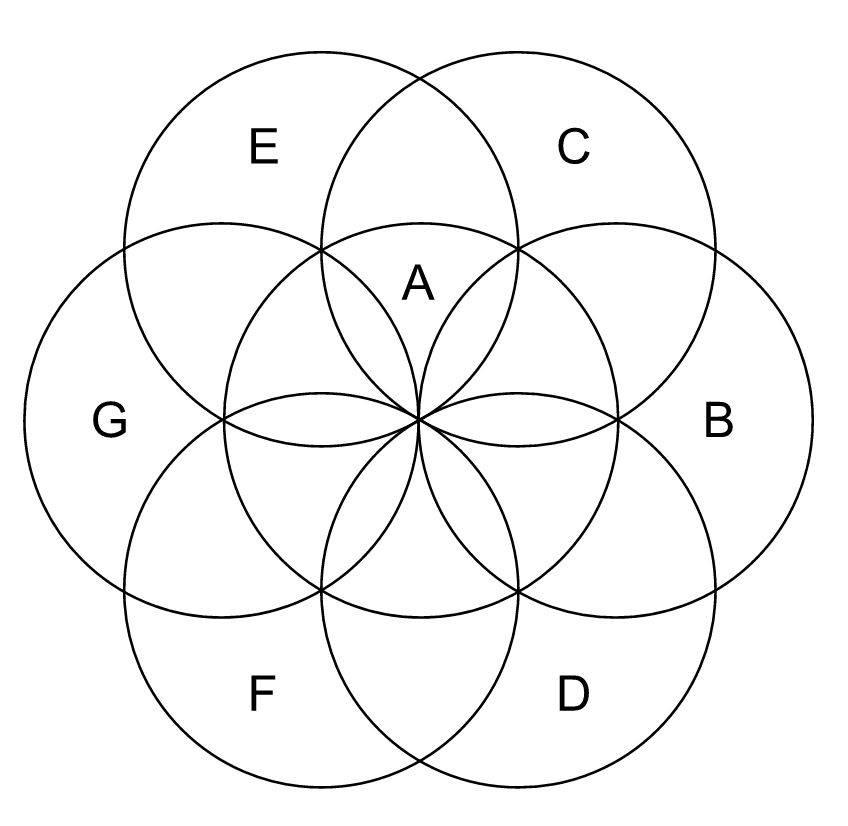
The most apparent new feature, in this stage, is a six-pointed figure in the middle of the geometrical construction. In art and archeology, the figure is called the six-petal rosette. We can now see how easy it is to create it, and this explains why it has been so widely used over the millenniums all the way until our days.

I have not collected items containing the six-petal rosette simply because they are far too numerous and could fill a whole book. A good source for nearly 300 pictures can be found from the dedicated 6-petal photostream¹⁴ on flickr.com. Recently, I found this symbol from medieval roof paintings (possibly 1400 AD) in the Porvoo Cathedral¹⁵, Finland. The symbol is combined with flower and spiral motifs, which can be seen below:

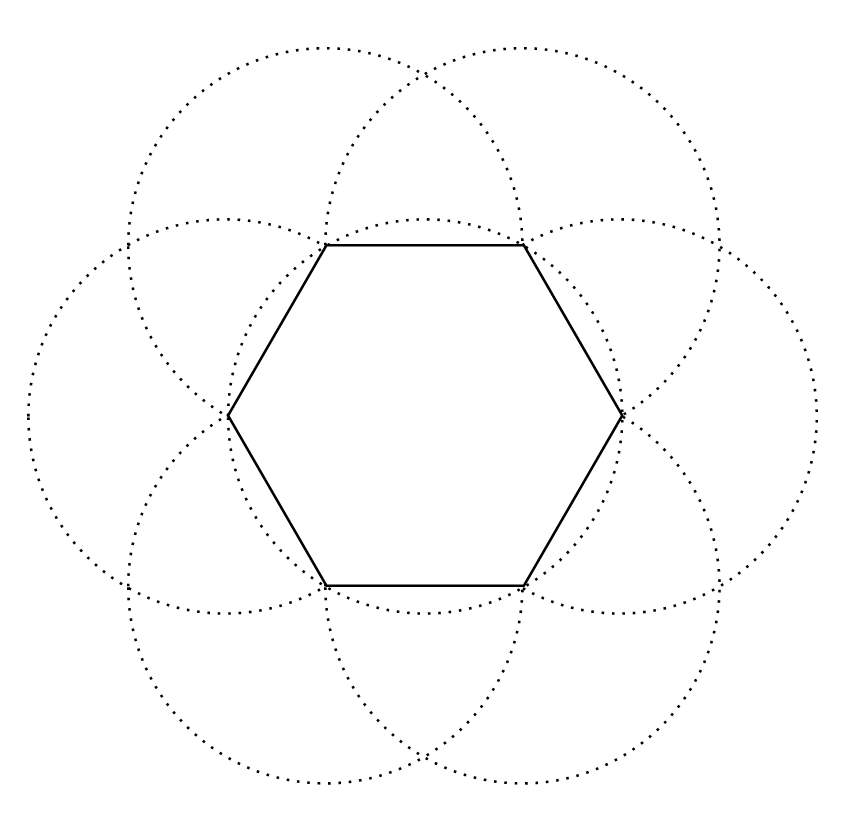
Three more figures worth noting are found when connecting six intersecting points of the previous figure with straight lines. They form the hexagon (picture 4.3.10), the hexagram (picture 4.3.11), and the six-spoked wheel (picture 4.3.12).

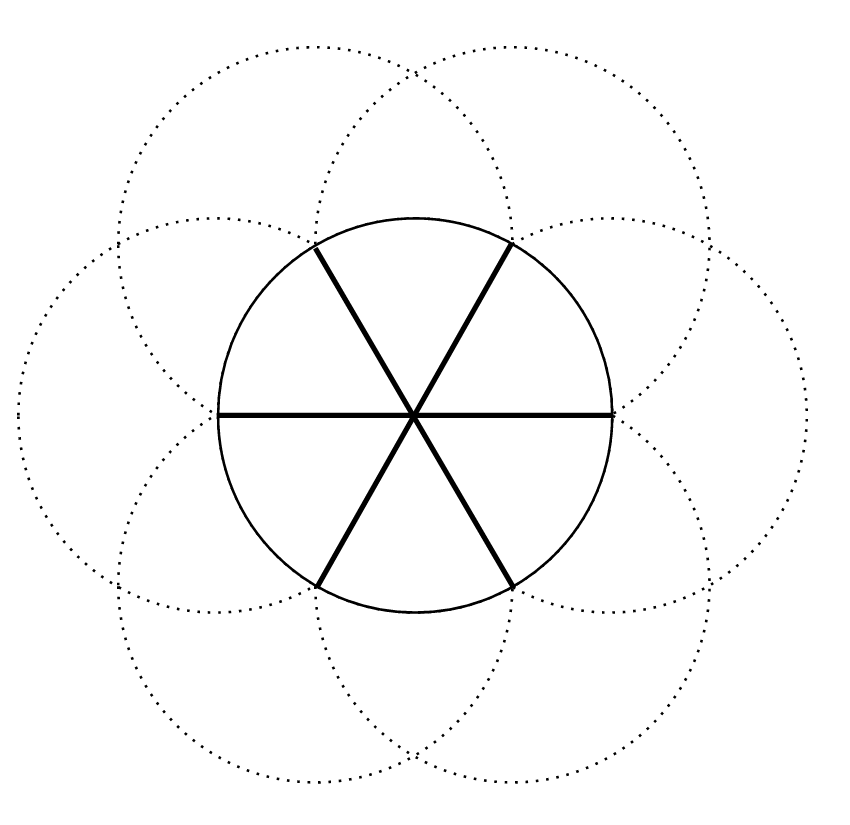
The figure in the middle, the hexagram is also known as the Star of David. The hexagram is often associated with Judaism, but satkona, as the hexagram is called in India, has at least equally long history¹⁶. It is still debated if the hexagram is a later pagan association stigmatized to the Judaism, for example into the flag of Israel. It is argued that more ancient and more genuine symbol was a seven-branched candle holder, the Menorah of the Temple. However, it is quite evident that numbers and symbols like the Star of David and the Menorah were unbreakably tied together. Mixed feelings towards the number six apparently came from early Christian apologists and their apocalyptically oriented facile interpretations of the number . Albeit more philosophically oriented Jewish thinkers like Philo Judaeus regarded the number 6 as a perfect number. Philo hardly thought anything evil or imperfect involved in the number six even the praise over the number seven is repeatedly stated in many of his works, for instance, The Special Laws II¹⁷:

But Moses, from a most honourable cause, called it consummation and perfection; attributing to the number six the origination of all the parts of the world, and to the number seven their perfection; for the number six is an oddeven number, being composed of twice three, having the odd number for the male and the even number for the female, from the union of which, production takes place in accordance with the unalterable laws of nature. But the number seven is free from all such commixture, and is, if one must speak plainly, the light of the number six; for what the number six engendered, that the number seven displayed when brought to perfection.

The geometric relations presented in this book, PIE and Semitic numerals phonetic intimation^{18 19}, astro-mythical association with the Pleiades, and symbolic attachment presented later in Part 2 shows that there are other natural explanations, which give significance to numbers and , , or its reciprocal ratio.

Six or seven?

The dominant presence of the six-spoked wheel sign in the Old Indus script from the third millennium BC suggests that the meaning of the six was imprinted deeply into the culture. The world leading specialist and professor emeritus of Indology, Asko Parpola associates the six-spoked wheel with the Sun.

Parpola also mentions that there is a group of six vertical lines with a fish symbol²⁰, which he associates with the Pleiades star cluster. The Pleiades was known to be close to the Sun at vernal equinoxes in the 3rd millennium BC. Both eastern and western traditions share the same identifiers of the Pleiades. Once the Pleiades (meaning "plenty" or "to sail") was seven sister stars visible for a naked eye, but then something happened and one of the stars disappeared. According to the Greek legend, Merope²¹, the disappeared star of the Pleiades, was having sexual intercourse with a mortal man and became invisible from shame²². The Pleiades was a crucial sign on the night sky for sailors and a seasonal sign of the spring equinox for farmers at the era of Taurus, the Sacred Bull in 4000 - 1700 BC²³.

It is speculated that there were supernova blasts at the moment of the disappearance of the lost Pleiades star which caused huge disasters in the northern hemisphere of the Earth²⁴. The sudden disappearance of the famous star must have had an impact on different civilizations. Was it a catalyst for changes in ancient civilizations and did it happen at the time of Taurus is just speculation, but strange coincidence with relation is perfectly fitting to the geometrical progression and historical evanescence of the FOL. According to Biblical chronology, the Great flood and collapse of the Babel tower are dated between 3000 - 2000 BC, which suggests that there has been another dark age that we are not totally aware of.

The importance of six and seven was so deeply imprinted in the cultural communication components (remember the division of cubit measurement units to Royal = palms and Mundane = palms in the Old Kingdom of Egypt or the same with the ancient Israelite long and short cubit) that people already in those times became unconscious of their detailed meaning. The structure of was an integral part of the communication systems, a tool to be used to understand, control, and measure circumstances, but nothing to be comprehended.

One more figure to illustrate the relationship between is presented below. If we draw a circle with a diameter (NQ) then the height of the Vesica Piscis (FG) is . Consequently, the area of the brown square is approximately . Half of the diagonal of the black square (Z₁P₁) drawn around the circle is or approximately as the full square diagonal.

Close connection to the number or halving factor as opposed to the number as a doubling factor is seen from the square of the which is , just one short of (or ). in Egyptian fractions is denoted by .

These whole number values are quite practical and can explain why had such an enigmatic position in ancient stories. In ancient sexagesimal (base 60) and modern decimal (base 10) number systems numbers divided by will give recurring decimal expansion, meaning that the outcome of the numbers divided by are not as easy to handle as others²⁵. Adding that has for long been used for pi approximation, which is why I think there are natural (mathematical and geometrical) reasons why has such an important role in myths. It can be seen as an invisible actor behind fundamental arithmetic relationships.

How does this relate to the study of the FOL? There are six circles around the First One which is in the middle and is connected to all other circles. This First circle is a reminder of the Primum Movens which is about to move to the background very soon leaving people to debate if there ever was such a thing called the First Cause and the Prime Mover. Or maybe there was, but it is not taking any action anymore, maybe it is just passively observing the thrive and the cease of the universe that it once set forth.

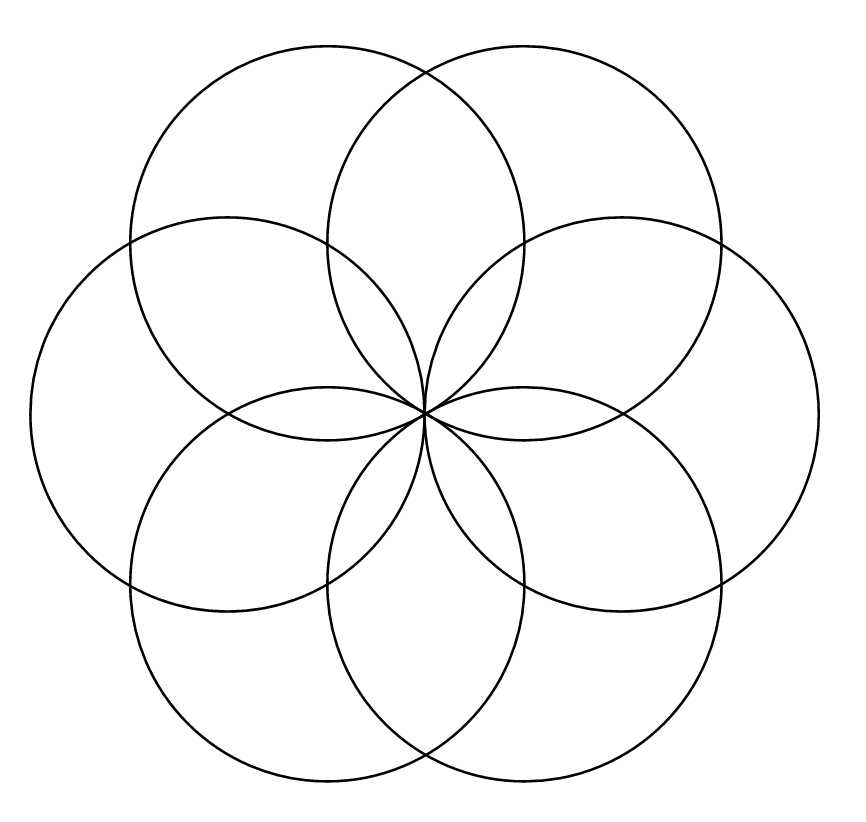
From the illustration above, we can notice how the first circle can be taken away from the center of the construction while still keeping the figure symmetric and complete. Although they are often cited, it is good to meditate these words from Genesis 2:1-3²⁶:

Thus the heavens and the earth were finished, and all their multitude. And on the seventh day God finished the work that he had done, and he rested on the seventh day from all the work that he had done. So God blessed the seventh day and hallowed it, because on it God rested from all the work that he had done in creation.

Number six seems to be the final complete and steady result at this stage, but we know that it was created by the help of the seventh circle in the middle. Thus, we can say that a total of seven circles is the greater base of the FOL while the first two circles forming the Vesica Piscis are the lesser base of the FOL.

When the center circle is included on the motif, FOL class 1 is formed because six more leaves encircling the six-petal rosette become apparent. On the outer edge of the hand-drawn figure above (picture 4.3.16), we can see six more intersecting points that urge us to repeat the procedure over and over again.

On the above figure (picture 4.3.17) we have finished the second round and encircled the motif with 12 leaves. This is the FOL class 2. Both class 1 and class 2 are common in the ancient mosaic art, ivory items, and wooden carvings.

FOL - symbol and pattern

When more circles and rounds are added, different levels of the FOL with certain mathematical properties will appear. I have classified these levels or stages in Appendix 1. There is practically no limit on levels we can go around and create new petals for the flower. Thus, we can think that the FOL is a dynamic, infinite process of thriving, producing, generating, and spreading. Flowering so to say. Every level holds seeds for the next generation. Seeds, centers of circles, are in the intersecting points at the outer edge of the formation. Intersecting points are wounds on the perimeter. There is a cut on the ground and a new seed is sown. The death and the disappearance of the seed on a planar field enable a new greater manifestation of the FOL.

We can now see the third round of drawing process of the formation of the FOL below:

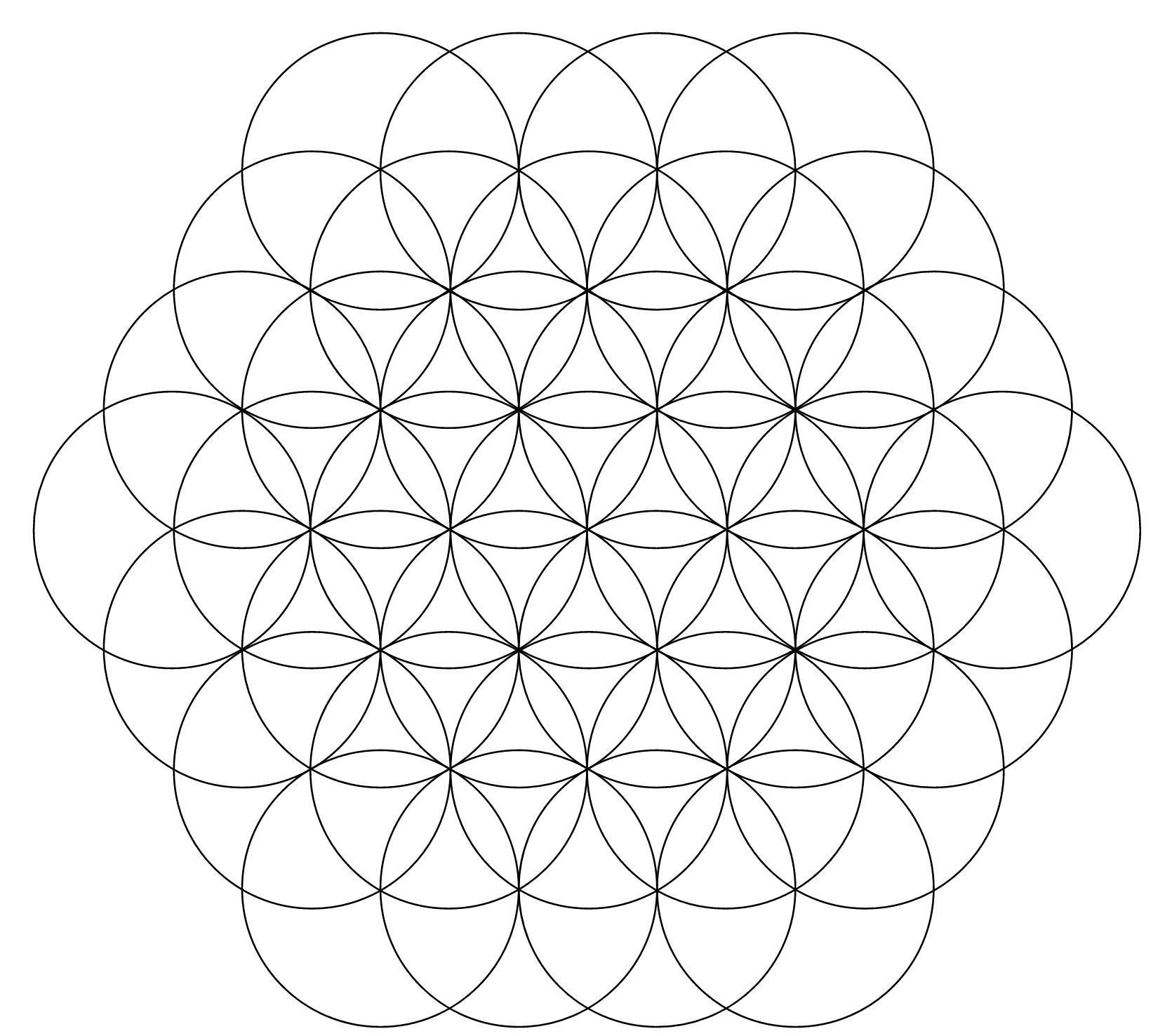
A very subtle but still important aspect must be noticed here. If the FOL pattern is continued further like this without the finishing step described below, we can rather speak of ornamentation than the symbol itself. If we finish the picture by filling 18 outer leaves of the hexagonal shape of the figure and remove the leftover circular arcs, we will end up getting a well-defined, clearly elaborated, consciously bordered symbol (see picture 4.3.21). This way we can make a distinction between an ornament and a symbol.

But this does not mean that an ornament can't act as a symbol, even if it itself might be constructed from repeated symbols. One can see this ornamentation defined to a higher category, analogical to a decryptable non-verbal sign of intercultural communication as described by Nadezhda Nikolenko²⁷:

The nature of any ornament is twofold: being a sign-index, a direction indicator in the intercultural communication process, at the same time it is a symbol. It contains cultural messages of communicating ethnic groups in a compact form.

...

It means that in order to facilitate the understanding of the symbolic structures' meaning, we should find analogues of the element in the culture of the recipient. For example, some symbols of the nomadic ornament may have analogues in the ornamental culture of settled folks (astral, solar and plant symbols). Then, in the case of effective intercultural dialogue and with the direct participation and leadership of the communicator, the recipient may have a possibility to learn to interpret adequately the transmitted ornamental symbols.

Cow who ate a flower

Knowing the simplicity of the construction of the FOL, it is confusing to find out that the four-petal lattice, the Cownose pattern (akk. apsamikku), outscores the FOL by being a far more common in Sumerian and Indus cultures. The popularity of the Cownose over the FOL can still be witnessed in Greco-Roman mosaics. The Cownose seems to be the most analyzed ancient geometric form by modern researchers as well. In books about Old Babylonian mathematics and geometry, authors tend to use most of the effort (Duncan Melville, Eleanor Robson, Tom Zara, Jöran Friberg) to the Apsamikku (we may follow an endless debate over the name) and only casually mentioning the six-petal rosette, Vesica Piscis or . For an additional example, R. P. Kulkarni mentions Mackay (1948) demonstrating a 12 division base of the four-petal rosette on the Plate XVIII²⁸ which dates to 3rd or 2nd millennium BC Indus culture. The exact dating is hard to deduce from the text. But again, the Cownose gets the full attention.

However, E. Robson in Mesopotamian Mathematics, 2100-1600 BC²⁹ mentions Kilmer (1990), who clearly states that the Apsamikku concept may apply to the three sided geometrical figure as well. Coefficient list on page 50 further shows that a-pu-sa-mi-ik-ki sa 3 refers to the concave triangle figure. This is probably the closest we can get to the name which ancient Babylonians have used for the FOL-like pattern: Apusamiikku. And this is the standpoint from which I am further developing the theory of the meaning of the FOL in Part 2 of this monograph.

Ancient Edakkal caves in India give an impression of Neolithic people trying to figure out the difference between concepts of dividing a circle to six or to eight parts. Picture below was kindly provided and permitted for use by Tes³⁰:

Wiki page states the ancient history of the caves:

Edakkal Caves are two natural caves at a remote location at Edakkal, 25 km from Kalpetta in the Wayanad district of Kerala in India's Western Ghats. They lie 1,200 metres above sea level on Ambukutty Mala, beside an ancient trade route connecting the high mountains of Mysore to the ports of the Malabar coast. Inside the caves are pictorial writings believed to date to at least 6,000 BC, from the Neolithic man, indicating the presence of a prehistoric civilization or settlement in this region. The Stone Age carvings of Edakkal are rare and are the only known examples from south India.³¹

These separate but connected ideas of the binary and the trinary division of wheels are crucial in order to understand the development of the Cownose and the Flower of Life patterns further. Philosophically the sequence of the square root 2 and the square root 3 was developed by Plato in Timaeus, where he speaks of Anima Mundi or World Soul and sets up the concept known as "Plato's lambda". It is a simple right and left handed sequence of numbers starting from:

a) 1, 2, 4, 8,...

b) 1, 3, 9, 27,...

These doubling and tripling sequences are nothing but powers of the square root of 2 and the square root of 3. In the Common Era, Philo Judaeus and Didymus the Blind developed these sequences accordingly finding that the seventh item of the sequences, namely 64 and 729, happened to be a square and a cubic number simultaneously³².

Mythologically these two sequences are coherent with roots of the trees better known as the Tree of Knowledge and the Tree of Life. The Tree of Knowledge is an ability to distinct between good and evil, i.e. the difference in existence. The Tree of Life serves as a unifier, i.e. the sameness on existence. Ernest McClain has gone deep to the realm of this idea in his excellent book The Pythagorean Plato: Prelude to the Song Itself³³.

Oldest reference to the FOL pattern so far

In his book on pottery styles, Gonzague Quivron presents an interesting collection of floral motives developing from early to mature stage³⁴ in the Indus Valley Civilization chronology. In the figure 16.8, the FOL pattern (class p) exists already in the Pre-Indus traditions, before Mature Indus period, i.e. before 2500 BC. But then the FOL disappears from the motif samples while the Cownose motif (16.9) appears practically on every stage. A partial screenshot of the figure 16³⁵ can be seen below:

Although not totally satisfactory, because I have not found the actual artifact, nevertheless, this is the earliest reference to the FOL pattern I have found after my earlier research in 2014. I expected to find the earliest references to the FOL at around 2000 BC from Mesopotamia, but instead the earliest reference is the ancient Indus ceramic pottery decorative motif from the middle of the third millennium BC. From now on, it is just a matter of debate between historians and their schools; if we can expect that the FOL ornament was really invented in India, or if it was borrowed from Mesopotamia, thus making the dating of the FOL symbol to be even earlier than 2500 BC. The next occurrence of the FOL in India is the Bedse cave arch decoration³⁶ on a Buddhist temple in Maharashtra, India, 200 BC.

A gap of over 2000 years in the recorded FOL findings in India must be partly because artifact samples are from books and media which are provided by individuals and organizations who have paid no attention to the FOL motif itself. The FOL motives are left out from printed materials, they are just not brought to publicity. Yet, I want to believe. Another historical reason for the lack of interest toward the FOL might be that the FOL pattern became part of an esoterizing phenomenon, where certain intellectual structures related to subtle angulation of 60 degrees, confusing parity, the disappearance of the seventh star of the Pleiades, etc. altogether perished from the radar of the public eye. These structures, rather than disappearing totally from the culture or becoming a subject of secretive speculation, became an integral part of cultural communication systems, myths, and tools. They were not an object of investigation, they had become banal, too apparent and close for people to be astonished about anymore.

Another innate reason for Cownose being more common is the straight edge appearance and origin of the symbol. Setting lines on a 90 degrees' angle, crossing them like ╳ is easier to do than the subtler 60-degree angle. We could find out the right angles roughly with our eyes, the right angle will lock in and please us immediately. Right angled forms like swastikas can be traced back to 10,000 BC. Eight-spoked ivory wheels from Sungir suggest that 2-fold rotational symmetry was appreciated even 30,000 years ago!³⁷ For a triangular orientation, some tools, calculation, or practice must be done in order to come up with a precise solution. There is more struggle with it. Trisecting an angle is a very famous ancient Greek geometric problem that is impossible to solve by a straightedge and a compass³⁸. Thus, my theory is that the quest to find a 60-degree angle is a result of further development of the structural understanding of the world, the sign of higher resolution capacity of the human mind. Although, as a geometric construction, a triangle comes first from the intersection point of the first circle and the second circle perimeters, the human knowledge and the comprehension evolve later to understand triangularity.

But now it is time to complete the FOL class 3.

FOL class 3

In the picture below, leftover and erasable arcs are faded by gray dotted lines leaving 18 outer petals as a border of the hexagonally shaped symbol. Black solid lines present the final symbol, the Flower of Life class 3:

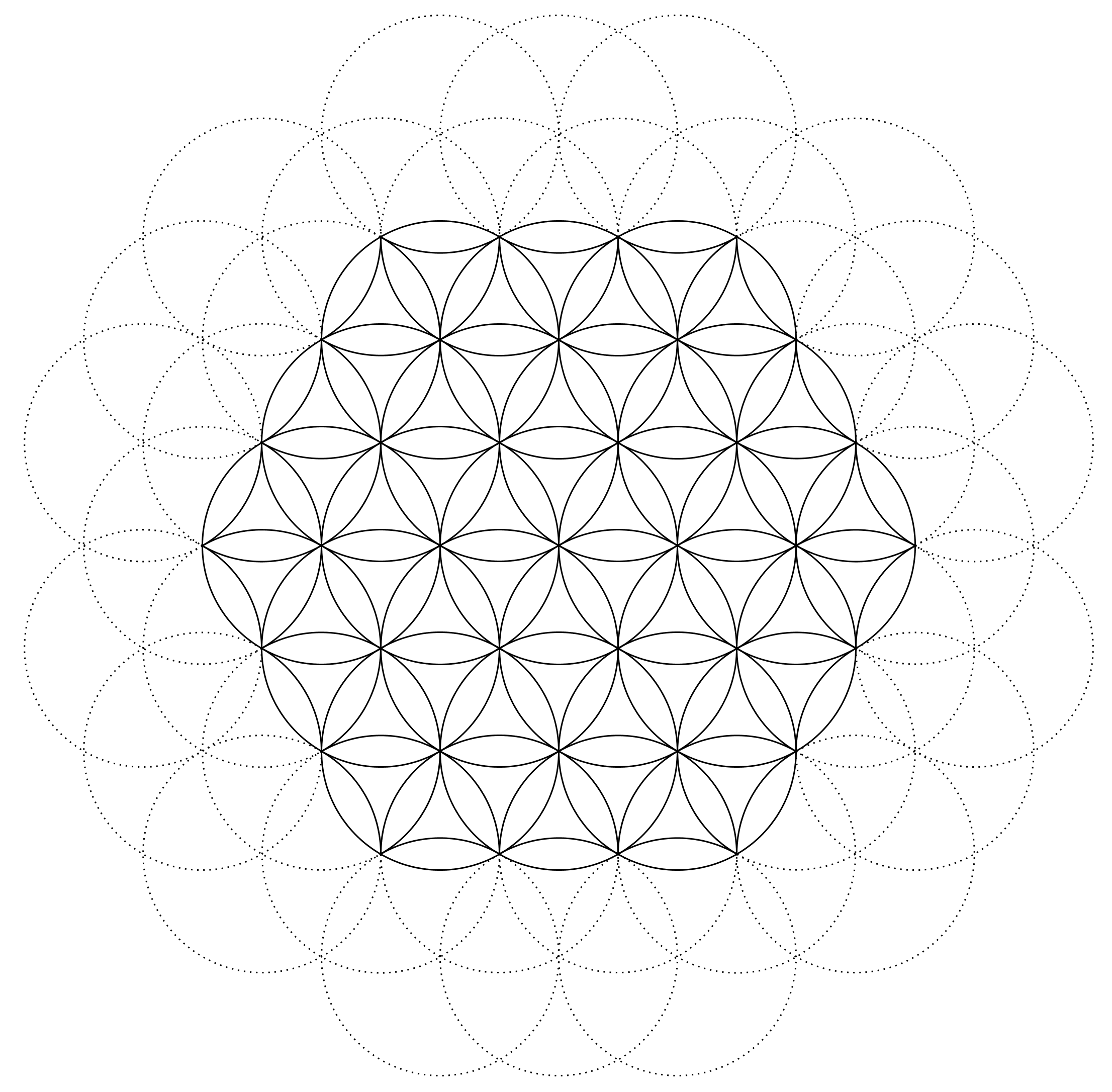
Although sometimes used as an ornament and as a pattern (particularly on class p artifacts), my take is that the FOL also has a strict symbolic form. This comes apparent by enclosing arcs, which are notable for class 1, class 2, and class 3 illustrations. We can often see the final symbol placed on a circular object, to places such as the bottom of goblets, vases, and whorls. Or alternatively, the FOL symbol might be encircled with a deliberate border, like on mosaics. In his books³⁹, Drunvalo Melchizedek pays a great attention to the limiting additional circle around the symbol. Seemingly, the border that is used will affect some mathematical ratios that we can see in the FOL. In the picture below, the bigger interior circle around the motif is in contact with the six outermost smaller circles. The bigger exterior circle finalizes the symbol as it was described by D. Melchizedek. This concludes the formation of the symbol in Part 1 of this complementary document focusing on the formation of the FOL symbol.