From a line to a plane
Chinese "Yin and Yang" -figure (on the left) is a beautiful geometrical symbol which contains the idea of opposite seeds. We can see a white seed on the black background and a black seed on the white background in a relationship that enables everlasting change and mutation.
Not only two is apparent on a line, but also two points (A & B) and the relation between them, or one segment with two ends, are giving three "things" at once. Is this the reason why ancient arithmeticians did not regard one and two as numbers at all, but rather said that three is the first real number? A subject, an object, and the relation between them, they all are included simultaneously in the conscious act of the investigator.
Triangle and square
When the space between two points, A & B is maximized, Prime Mover1 needs to find new ways to introspect. Instead of increasing what already is a maximum distance from A by moving forward, or decreasing the distance by moving backward on the line, Prime Mover causes a movement to any other direction C with an angle X. And like magic, the first and the simplest of two-dimensional shape between all points (A, B, and C) is created, a triangle:
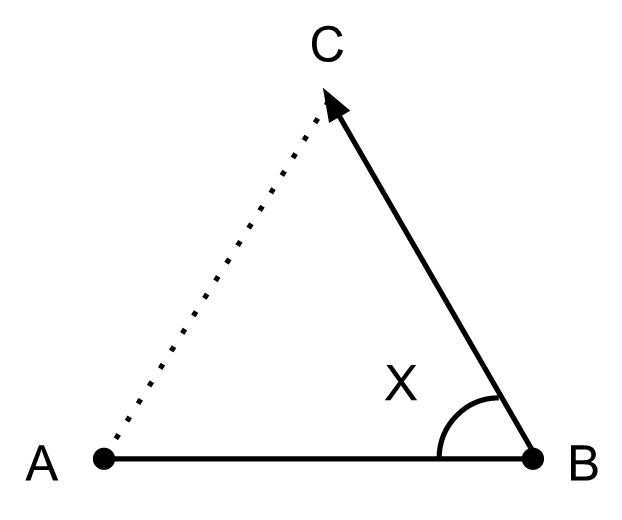
The shape of a triangle2 can be any and is related to the side lengths and angles of a triangle, but for simplicity and suitability for our theme, we have presented an equilateral triangle as above. Another common way to describe this dimension is by projecting the line CD parallel to the line AB so that it creates a square:
There are several different shapes that four lines can make3, but we will focus mostly on a square and a rhombus.
Circle
Triangular, quadrilateral, or any polygonal shapes exist in this two-dimensional world. And so does the shape that is the source of all mysteries, a circle. Consider a line constructed from points A and B, where A is stationary and B moves. If we take a single direction other than backward or forward, we keep the distance to the stationary point A the same, and we keep moving then a circle will appear:
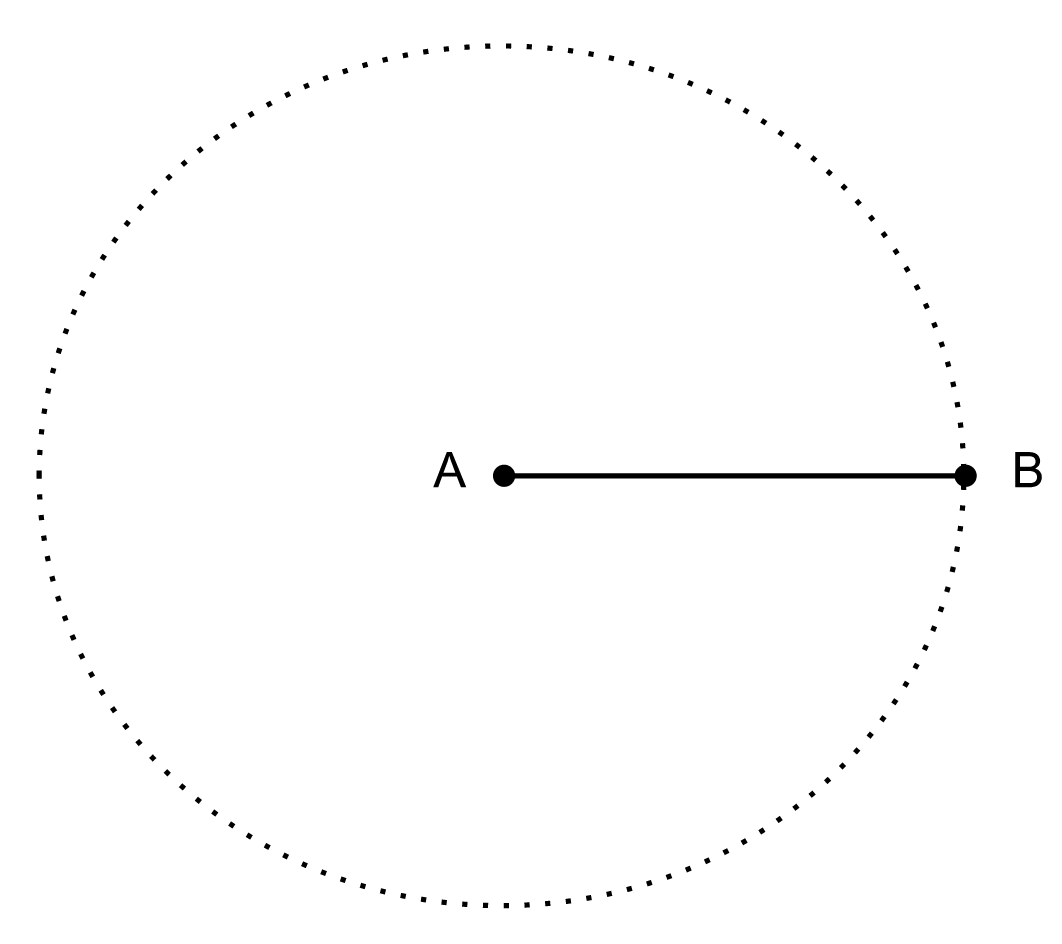
By changing a few factors like adding center points or changing the length of the radius, we can draw different types of circles and ellipses.
We do not really know when people have started to use steady or adjustable drafting compasses to draw perfect circles like this. A certain time period of the Indus civilization, the Mature Harappan civilization (2500 - 1900 BC), contains a lot of historical evidence in pottery paintings that certain instruments were used to draw circles4. Instead of finding the source of the invention of the compass from rounded pottery and their circle oriented decoration or stone circles from Neolithic times, one could see further to the dawn of agriculture when animals were domesticated. It was usual that goats and similar animals were tethered to a center pole. When the goat ate grass and stamped the ground around the pole, it can be seen how a circular area was formed5. This can be imitated easily on a smaller scale with a center stick, a wire, and a pen.
Anyway, from the formation of a triangle, a square, and a circle we can see how many new things happened and from what started simple is getting more complex now. Still, we should see how everything evolves from a single point, extends to a line, and finally to a plane. Traditionally a plane (a surface) is defined as a line with width and a solid as a plane with height.
Angles rising from...
The point actually has the second planar dimension in its very etymological nature. Sharp edges of the triangle, corners of the square and degrees of the circle are turning points on a plane that create angles. As we remember, sharp sounding ak- and ok- PIE syllables are related to the point etymology, whereas softer ank- and ang- syllables6 are often related to corners and angles. Conifer7 cones8, very ancient and widely used symbol in the Assyrian art, are directly pointing to or carrying these angles and sharp edges in their botanical etymology.
Angle is the new notable feature in the second dimension that should be carefully contemplated. When two lines intersect with each other they form a certain relationship. Say the line a is a straight line going through points A and B. The line a will act as a reference from now on. The straight line b will go via points A and C. Now both lines will meet at the point A, thus forming an intersection point. The special relationship that the lines make at that point is called a slope or a ratio by the fact that for every three horizontal steps (a run) the line a takes, the line b will increase its vertical value by two (a rise).
Thus, the ratio is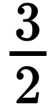 
or its reciprocal ratio 
, depending on which is the property we want to compare to, a width to a height or a height to a width. Generalizing this idea, Thales, the famous mathematician from Miletus (around 600 BC) found out that he can deductively calculate the long forgotten and the impossible to measure the height of the Great Pyramid based on the height of himself, the length of his own shadow, and the length of the shadow of the pyramid at the certain time of a day9. This forms the very base of the logic itself because using ratios (that is: defining relations) and proportions (that is: using analogies), logical reasoning is possible. In fact, logic or logos as ancient Greeks called it, is an actualized proportion.
...deep waters
In mythology, divine reasoning or just the law is best described by angling (fishing with hooks) and fishing with nets. The bigger the fishes are, the more cosmic and orderly principles of the creation process they are meant to describe. Half a fish and half a man creatures appear in many ancient cultures. In Mesopotamia and Egypt, Abyss or Ab is the primordial sea (Thalassa10 in Greek mythology), where Dagon11 or Aptu12 (transformed Isis in Egypt) rose up to teach mankind. Controversial Flower of Life symbols, which are shown in the previous research, are found from Abydos, Egypt. The Apsamikku (or ab-za-mi), the other "Flower of Life" symbol discussed later in this paper, may refer to a window or to a hole leading to the deepness of the ocean. Order of points in the triangle ABC has a strange correspondence to the name syllable of the deepness ABS / ABZ. This seems to remind us that the alphabetical system has been empowered with the creation principles of the ancient myths.
These are very powerful ideas derived from a geometrical angle. But let us get shortly back to the botanical field. A plain flat and thin surface, or a plane as described in mathematics, has etymological roots in a sacred Western Asian broad-leaved plane-tree, Platanus orientalis13. As Victor Hehn mentions, it was under the plane-tree where Plato seats his teacher Socrates and Phaedrus for a chat14. Was it fanciful Plato thinking of himself as a cover and soothing his dear protagonist Socrates and interlocutor known from many dialogues, Phaedrus15 in a torrid Mediterranean day? We may not know the reason, but we can be sure that it was an ideal place for a conversation of the mastermind and geometry lover, Plato. In one sense Plato further developed the proportional discovery of Thales. Not only was truth reachable by using analogies, but actually the world of logic or Logos was the only true world, making the sensible world only a reflection or a shadow of the immaterial world.
On this plane, we can finally draw a plan for the central figure in question, the Flower of Life.